Altered States
In my last article (Extended Chords) you learned how to form extended chords; this time we’ll figure out how to alter them. Any note can be altered in a chord, but not all alterations will lead to an “altered chord.” That’s because we have easier ways of noting certain alterations – let’s look at each scale note in turn:
Roots – if the root is altered, the chord changes names. Chord names have two parts – the root name (given as a letter) and a quality name that describes what’s happening above the root. Since every chord is identified from the root, a C major chord with a raised root (C#-E-G) would be called a C# diminished chord; an F minor chord with a lowered root (Fb-Ab-C) becomes an augmented chord on the new root (E-G#-B#). Changing the root in a complex chord structure can lead to an altered chord, but it’s never the root that ends up as the alteration.
Seconds – in traditional harmony, chords are built in thirds. The second is the same note as the ninth – the note right after the octave – so it’s always called the ninth. Beginners make a common assumption that calling a note a ‘ninth’ means it’s in a different octave, but that’s not the case – it’s called a ninth even if it’s the lowest tone in a chord, and even if the root is in the same octave.
Ninths can be raised (#9) or lowered (b9).
If the ninth is used in a chord, you’ll also know if the chord contains a seventh – chords like C9 or Am9 always include a flatted seventh; chords like Bbmaj9 always include a natural seventh, and if there’s no seventh at all, it’s an ‘add9’ chord. You’ll sometimes see chords noted as ‘sus2’, which implies the third has been replaced by a second; although I disagree with this naming, that’s beyond the scope of this article – at least you’ll know what’s implied.
Thirds – if a third is lowered, the chord is called minor; if a third is raised, it’s the same tone as the fourth – a suspended chord. Since we have easier ways to indicate the alteration of a third, you’ll never see it altered.
Fourths – if you lower the fourth of a chord, you end up with the same note as the third. Consequently, you’ll never see a chord with b11 – chords that include both a natural third and a flatted third are written as a major chord with a #9. If the fourth is raised in a chord, it’ll be indicated as #11 or +11.
Fifths – these can lead to altered chords in half the cases. Raising the fifth in a major chord gives us an augmented chord (1-3-#5), and lowering the fifth in a minor chord gives us a diminished chord (1-b3-b5), so fifths can be an altered tone only if they’re raised in a minor chord (example: Cm7#5) or lowered in a major one (example: C7b5). In the past few years, the m7b5 has replaced the half diminished chord in most charts, so that’s the exception to the rule.
Sixths – These are only called sixths if there’s no seventh present. You should never see a ‘Cadd6’ chord – it’s simply C6. If the seventh is present in the chord, the sixth is called a 13th . Raising this note gives the same tone as a flatted seventh – and that’s implied in a 13th chord – so you’ll see b13, but not #13.
Sevenths – if a seventh is lowered, the result is a dominant chord, simply written with a number… lower the seventh of Cmaj7 and you get C7. Raising the seventh gives you the same note as the octave, so Cmaj7 with a raised 7th = C major.
Since that completes our tour of the notes, I’ll recap what can be altered:
- Root – never
- 2nd /9th – you’ll see b9 or #9
- Third – never
- 4th /11th – you’ll only see #11
- Fifth – sometimes; you’ll see b5 or #5
- 6th /13th – you’ll only see b13
- Seventh – never
That gives us a total of six altered notes: b9, #9, #11, b5, #5, and b13. Even better, the #11 and b5 are the same note – and so are the #5 and b13! That means all altered chord fingerings are going to have one or more of the following:
- The root tone raised one fret to make b9
- The third lowered one fret to make #9
- The fifth lowered one fret to make #11 or b5
- The fifth raised one fret to make #5 or b13
That’s it in a nutshell – four possibilities. Doesn’t seem quite so scary now, does it?
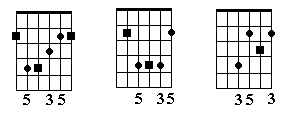
In my last article I talked about the importance of knowing where the basic chord tones are in voicings – here’s a quick review – roots are shown as squares:
If you’ve learned how to form extended chords, and you know the root, third, and fifth in each fingering, you can form any altered chord – no matter how complicated!
You’ll need to be careful about one thing, though – some voicings have notes doubled. In the first two diagrams, there are two fifths – if you alter one to make a b5 or #5 chord, you’ll need to get rid of (or change) the other one. Altered 9ths (b9 or #9) can include the natural third, and b13 chords include the fifth, so it’s only doubled fifths you’ll need to worry about, and only when the fifth is an altered tone.
One quick word about chord symbols before we dig into examples: a “+” means the same as a #… unless it’s at the end of a chord name; then it means a raised fifth. In other words, G9+ is 1-3-#5-b7-9; G7+9 is 1-3-5-b7-#9. You’ll see either plusses or sharps in chord names, and sometimes both (as in G7#11+). A minus sign doesn’t mean a flat, though… if you see one of those, it means the same as ‘minor’.
Now we’ll see how this works in practice… I’ll just show one possibility for each voicing – you can refer back to the extended chord article to construct others.
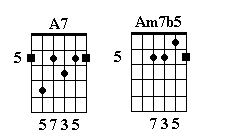
Am7b5
Start with one of the A seventh forms (see the article on extended chords), lower the third to get a minor, and lower the fifth to complete the chord:
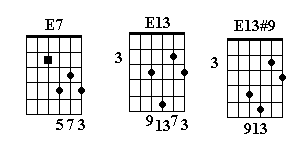
E13#9
Lower third by one fret, or raise a root by three to get the #9 – having both the third and #9 in the voicing gives it the tension of that raised ninth. If you’re starting with a 13th chord that includes the ninth, just raise it a fret:
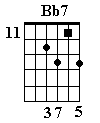
Bb7#9+
From a seventh form, lower a third by one fret (or raise the root by three if you’ve only got one third), then raise the fifth:
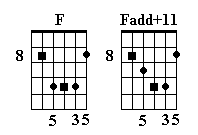
Fadd+11
To an F major chord, lower a fifth by one fret. You’ll want to use a voicing that begins with two fifths:
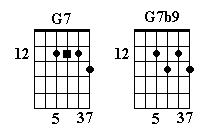
G7b9
Using a seventh form, raise the root by a fret:
(Did you notice that the top four notes of G7b9 form a diminished 7th? More on that in a minute!)
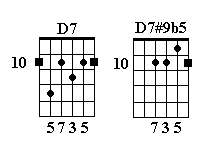
D7#9b5
From a seventh form, lower a third by one fret and lower the fifth by one:
Ok, I already hear some of you screaming that it can’t be – the 7b9 voicing is a diminished 7th, and the 7#9b5 I just showed is identical to the m7b5 fingering I gave earlier!
A couple of things about altered chords: first, they tend to have five or more tones if you played the ‘real’ voicing (many of which are unplayable on the guitar), and some tones are more important than others. It’s common to drop notes from altered chords, just as we did for extended chords. Let’s look at that last pair, the m7b5 and the 7#9b5. You’ve got:
Am7b5 = 1-b3-b5-b7 = A-C-Eb-G
and
A7#9b5 = 1-3-b5-b7-#9 = A-C#-Eb-G-B#
since B# is enharmonic to C, we can re-write that as A – C -C#- Eb – G … see how that actually contains the m7b5 tones?
Ah, but it won’t sound like a #9 without a natural third, will it? Well, you could use a voicing that includes both:
but you’ll be limited in the number of positions you’ll be able to play – and leaping all over the neck to grab the ‘right’ chord doesn’t lead to smooth changes.
The other big factor is context. Since it’s the 9th being altered, the odds are pretty good that the progression is leading your ear towards a major/dominant chord here – playing the minor will give you the #9, creating the effect in the context of the piece most of the time.
There are actually a few ‘cheats’ like this you can use. I find it easier to think about the altered chord tones since there are only four possible notes to alter, but you might prefer thinking of substitutions. Here’s a couple examples:
C7b9 = C-E-G-Bb-Db Gº7 = G-Bb-Db-E
C9#11 = C-E-G-Bb-D-F# Gm/maj7 = G-Bb-D-F#
Certain guitar voicings, because notes are left out, also work – if you look at the highest four notes in the last diagram you might recognize a voicing of Eb13:
A7#9b5 = A-C#-Eb-G-B# Eb13 = Eb – G -Bb-Db( C# )-F-Ab-C( B# )
Even though Eb13 is not really a substitute – the other three notes all clash with the A7#9b5 – the four notes in that particular voicing are a perfect fit!
You can even take simplification to extremes, grabbing the highest note, any altered ones, and whatever else fits…
C13b9 = C-E-G-Bb- Db -F- A Db+ = Db-F-A
but the more you take away, the more you’re trusting other instruments will fill in the blanks. If you’re at the point of knowing the notes in a 13b9 chord well enough to figure out the chords it contains, you didn’t need this article anyway!
In the next article I’ll talk about how altered chords are used as substitutions.