From Math to Music – A Mathematical Approach to Learning The Fret Board
One of the more difficult tasks to learning the guitar is mastering the fret board. Most beginning guitar lessons will point out a few relationships, then direct you to start memorizing the alphabetical sequence of the notes along each string. For some, this will come easy. But others will find this task intimidating. And it is at this point that many will give up their dream of learning guitar. Those that persevere may continue to struggle, and find note retrieval clumsy and slow. But there is a better way that employs simpler memorization and your ability to quickly add small integers in your head. The first part of this article will present this method, and the second part will provide additional information to reinforce your learning of the fret board.
Now the key to learning something new and seemingly complicated, is to discover relationships with the material using information you already know. We are going to learn the fret board by observing some of its hidden mathematical relationships. Then we will use our ability to quickly add small numbers in our head to speed up note retrieval and our memorization of the fret board.
First, the simple memorization part. To begin, we need to memorize the numerical values of all 12 notes of the chromatic scale. Simply number A to G#, sequentially starting from 0 and up to 11 as follows:

Now we know that the transitions from sharp to flat are enharmonic and represent the same note. Usually when ascending, the sharp notation is used, while descending, the flat notation is used, but for our purposes, it really doesn’t matter which notation you favor.
To help speed your memorization of each note value, pay particular attention to the number assignments given the natural notes A-B-C-D-E-F-G (0-2-3-5-7-8-10). Then if you need to “sharpen” a note, simply add 1. If you need to “flatten” a note, subtract 1. Note that there are no sharps or flats between B & C (2 & 3) and E & F (7 & 8).
At this point, you already know the fret that must be pressed to obtain all the notes along one string! Take a look at the A string.
Before we continue, you really need to commit to memory the values of the open-string notes on your six string guitar. That is, E-A-D-G-B-E is represented by 7-0-5-10-2-7. To help remember this sequence, think “0-5-10 between 2 7’s”. Note that the B string value is simply its string number and the A string has a value of 0.
We can use the sum of the string value and the fret number to solve for our note. Now, when you push down a fret and pick a string, just add the fret number to the string value and your result will correspond to your note. But if the sum of the string value and the fret number is 12 or greater, you must subtract 12 from your result until your number is from 0 to 11 in order to get your note.
For example, if I hold down the 4 th fret of my E string (value 7), then my sum is 7+4=11, which corresponds to G#. Of course, your speed at this will be strongly dependent on how well you committed the note values to memory. For example, when you see “D”, you need to instantly think “5”, and you need to do this without counting from 0 (A). But you will find that making this association is certainly a lot easier than trying to memorize every note along each string, or trying to count alphabetically from the open string note.
But what if the sum of the string value and the fret is 12 or greater? In this case, you will have to subtract 12 from your sum until you get a result from 0 to 11. For example, if you press the 10 th fret of the G string, your sum is 10+10=20. Simply subtract 12 from 20 to get 8, and you see your note is F. If your result is 0, that means don’t push a fret and play the string open to get your note. Refer to the following note map and try this for other notes along the fret board:
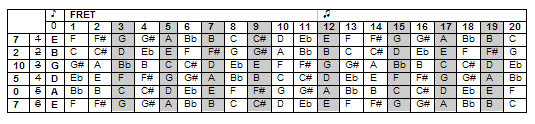
Well, this method easily tells you how to find the note you’re playing, but what you really need is a method to tell you what fret you must press to get the note you want. To use it this way, use the note value that you memorized and the string value you are on to solve for your fret number. Now if your note value is less than the value of the string you want to play it on, you must add 12 to your note value and subtract the string value to get the fret number to press.
For example, if you want the D note on the B string, you know that D has a value of 5 and the B string has a value of 2. To determine the fret number, simply ask yourself “What number must I add to 2 (the B string value) in order to equal 5 (my note)?” The answer is 3, so you press the 3 rd fret of the B string to get 5 (D note).
But what if the note you are looking for has a value less than the string value you wish to play it on? In this case, you must add 12 to your note value to solve for your fret number. For example, I want the B note on the G string. The B note has a value of 2, while the G string has a value of 10. So I must first add 12 to 2 to get 14. Then ask yourself, what number must be added to 10 (G string) to get 14? The answer is 4, so you press fret 4 of the G string in order to get your B note.
Of course, this will take some practice, but what you will soon discover is that it will actually speed your memorization of the fret board and your ability to randomly access your notes. Eventually you will just know where to go, almost without thinking about it. After you’ve memorized the value of each note from A to G#, as 0 through 11, you should practice trying to retrieve each note on each string.
For example, start with A and find A on each string, then try Bb, followed by C, and so on, for every note. Think of each string in terms of its open note value. Your fret board has markers at the 3 rd , 5 th , 7 th , 9 th , and 12 th fret. It also has marks at the 15 th , 17 th , 19 th , and 21 st fret. Use the fret board marks to quickly find your fret number.
So what is the significance of the string values? Note that 12 minus the numbers 7-0-5-10-2-7 (E-A-D-G-B-E) actually represent the fret number that must be pressed on each of the strings to hit the A note. That is, these numbers simply represent an index offset from 12 to the A note on each string.
Here are some other observations to help you navigate the fret board. We use the term “octave” to refer to the interval between two notes of which one note is at exactly twice the frequency of another note. When referring to the 12 notes of the chromatic scale, an octave refers to the 12 note transitions between a note and itself one octave higher. The same note one octave higher will actually have a string vibration (frequency) twice that of the original note. Thus, you know that by adding 12 to your fret number along any string will give you the same note one octave higher.
Now we have to establish a sense of direction. When I move up in pitch, I shift from the top string (low E string 6) towards the bottom string (high E string 1). Further, when I move up the fret board, I shift down the neck from the nut. The common element here is that shifting up corresponds to raising the pitch, even though I’m physically moving down the neck and down the strings.
Now that we got that straight, if you shift up two strings and up two frets, you will also get the octave of your note. But if when shifting strings, you happen to land on either of the first two strings (the B and high E strings), then you must shift up 3 frets instead of 2 to get the same note one octave higher. Now the octave of a note found by shifting 12 frets along the same string is equivalent to the octave of the same note found by shifting up 2 strings and 2 frets (or 2 strings and 3 frets if you land on the B or high E string).
So we see that every octave has a redundant position on the fret board. Further, we see that the fret board covers each note at least one octave above and one octave below it. Likewise, most of the notes also have a redundant position on the fret board. Note that the 5 th fret of every string (except between strings 2 & 3) is equal to the adjacent string’s note played open. We sometimes use this relationship to tune string to string after having tuned only one reference string. Now between strings 2 & 3 we must shift one fret lower – that is the 4 th fret of string 3 is equal to the string 2 played open. So with this in mind, the high-E string is actually 2 octaves above the low-E string. So how many octaves of low E can we find? What if you press the 12 th fret of the high E string? This is the 3 rd octave of low E. If your guitar happens to have 24 frets, then you can get the 4 th octave of low E as well.
Now you have a simple method for random note access, but with all the redundancy and note octaves, you still need to know that you’re playing the right note, or the right octave of a note. Without getting too complicated with regard to music theory, you know that symbols are positioned on the staff to indicate which note must be played. With respect to reading music, remember that the bottom line of our staff (5 lines) corresponds to the E note. Each staff line above or below represents a shift of two natural notes. Now with respect to the E note, we have another E one octave above and another E one octave below. With two note transitions for every line space of the staff, one octave on the staff spans the space of 4 lines. So E one octave higher is a span of 4 lines above the bottom line, E one octave lower is a span of 4 lines below the bottom line. So, what string and fret do we play for a symbol that intersects the bottom line of our staff? This is the E that occurs on the 2 nd fret of the D string (it also has a redundant position somewhere else). The E one octave higher will occur on the 5 th fret of the B string, or the again on the high-E string played open (remember the fifth fret is the higher adjacent string played open). So what about the E note that occurs on the 7 th fret of the A string? This is the same as the E played on the 2 nd fret of the adjacent D string (where we started). See the redundancy. Play the two notes on your guitar. If you’re tuned properly, they should sound the same.
Now refer to the note table and notice all the redundant notes as you move along the fret board! You must train your fingers to take advantage of this redundancy and always seek the path of least resistance when switching between notes. The next part of this lesson will help you to navigate note to note and identify some relationships that you can use to discriminate a note from its octave or its copy.
If you made it this far, here is some more food for thought that will help reinforce your memorization of the fret board (and it will even introduce you to the circle of fifths). In this next exercise, what we will attempt to do is to complete a fret map by noting the simple mathematical relationships that exist between notes on adjacent strings (and between adjacent notes arranged in the order of the circle of fifths).
Begin by constructing a table containing 6 columns and 12 rows. Number the columns from left to right to correspond to your strings from 6 to 1 (in order of increasing pitch). Label each row at the left with the 12 notes of the chromatic scale as shown below. Then place an 8 in the upper left-hand corner of your table at the intersection of the C row and 6 th string as shown below. The 8 refers to the fret you must press on the 6 th string to get C.
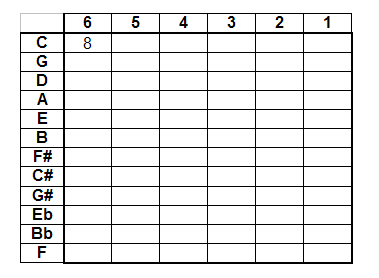
An easy way to remember the order of the 12 notes in the leftmost column is by memorizing the phrase:
Christian Girls Dig Angels Even Before Fat# Christian# Girls# Evenb Beforeb Flat
Note the pound symbol (#) after “Fat Christian Girls” that denotes a sharp, and the flat symbol (b) in “Even Before” Flat. The ordering of these notes is also significant, as it follows the order of the circle of fifths (more on this later).
Now what we want to do is fill out the table with the fret numbers that must be pressed in order to play each note at the left on the string above. But for the purposes of this exercise, we will not use the string values we learned in the prior lesson.
Instead, we will derive the fret numbers using the relationship that every adjacent fret number is found by either subtracting 5 or adding 7. We determine whether to add 7 or subtract 5 by obtaining a result that must be a number from 0 to 11. We know by now that the interval between the 3 rd and 2 nd string is always treated differently, so we will constrain our focus to the four strings at the left and doing the math starting from 8.
Using our relationship, the boxes adjacent to 8 must be filled by either (8-5) or (8+7). Since our result must be a number from 0 to 11, we choose to subtract 5 and our result is 3. So we place 3 in the two boxes adjacent to 8. Now the boxes adjacent to 3 are derived the same way. Here we choose to add 7 to get 10. Continue to fill out all the boxes of the first four columns this same way. For the last column (the high E string), we use the shortcut knowing that these fret numbers must be equal to the fret numbers of the first column (low E string).
Now we have one more column to fill. Derive the string 2 column by doing the opposite of what we did for the first 4 columns, and start from the last column (high E). That is, we will either subtract 7 or add 5 to each number in the rightmost column to get the adjacent number in column 2. Fill each box of column 2 this way. Now you should have a complete map that tells you what fret you must press to get each note of the chromatic scale on each string as follows:
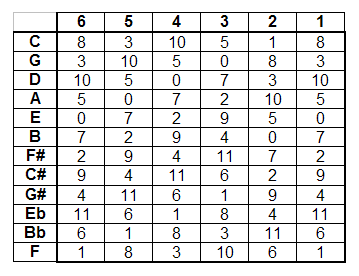
Bonus exercise – fill out the same table using the note values learned in the first part of this lesson.
So why did we do this? There are some patterns here that we can use. Note that for the first 4 columns, the adjacent column is found by shifting the numbers up one box and placing the number that shifted off the top, at the bottom of the adjacent column. Only between strings 3 and 2 are things handled differently. Here column 2 is found by shifting the numbers of column 6 down 1 and bringing the number shifted off the bottom to the top. But this visual pattern is not what I’m looking for. Instead, look at the fret numbers for the same note as we move across the strings. Notice that the fret always shifts by 7 or 5, except between strings 3 and 2, where it shifts by 8 or 4.
Now look back at the note table in the first part of this lesson. Note that if you pick a note on any string, and you shift up to the adjacent string (you shift up in the direction of increasing pitch), you get the octave of the note by shifting your fret up by 7 on the adjacent string. You get the redundant (copy) of the note by shifting your fret number down by 5. But if you are shifting from string 3 to string 2, you shift your fret up by 8 to get the octave, and you shift your fret down by 4 to get a redundant copy of your note.
Now referring back to the fret map, you can identify the octave shifts and the redundant copies using this same relationship. That is, as you up shift across the table, if the fret increases by 7, you hit the octave. If the fret decreases by 5, you hit a copy. This is true for any transition, except between strings 3 and 2, where the octave is found by up shifting 8, and the copy by down shifting 4. The following fret table uses the ^ symbol to identify a shift in octave as you shift across the strings:
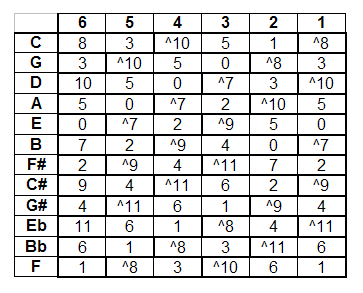
Notice that every note has two octaves as you move up in pitch from the low E string to the high E string (and you stay within 11 frets). Also note that there are a lot of redundant copies of notes, first octaves, and second octaves that you can take advantage of (the copies are bold boxed in the table). But if we are constrained only to the first 11 frets, some notes will not have a redundant copy (see low E, F, F#, G, G#–the first five notes on the low E string). However, every first octave does have at least one redundant copy. But not every second octave includes a redundant copy if we are constrained to the first 11 frets (see C, B, C#, D, Eb).
Because we already know that the sequence of fret and string combinations repeats itself one octave higher beginning at the 12 th fret, we have focused on all the note combinations formed up to the 11 th fret. We’re going to continue to focus on all the combinations up to the 11 th fret, but let’s take inventory. We know we have 6 strings and 11 frets, so this gives us 6×12=72 possible combinations of string and fret. Now, we’ve also seen that every note has exactly two octaves below the 12 th fret. 12 notes + 12 first octaves + 12 second octaves = 36. So we actually have 72-36=36 redundancies. That’s a lot to keep track of, but use the relationships we’ve identified to discern octaves and copies.
That is, as we up shift strings, we have a first octave by shifting 7 frets up on the first string shift, or two frets up if we shift 2 strings up (both of these octaves are equivalent). We have to make an adjustment on string 2 by adding 1 fret. We also have the copy of a note by down shifting 5 frets on the first string shift (or down shifting 4 frets to get the copy if we land on the B string).
So what exactly is the circle of fifths? We’ll save this for another lesson, except to say that in the circle of fifths, each adjacent note moving clockwise (starting with C in the 12 o’clock position) represents the fifth note in a major scale of the prior note. That is, G is the fifth note of a C major scale, D is the fifth note of a G major scale, and so on, moving clockwise around the circle.
I hope you found this information helpful. There sure is a lot of math in music! My hope is that by showing you some of these relationships, you can use this information to really get to know the fret board. Unfortunately, there are no shortcuts for practice, and to really affect your play, you simply have to practice.

Randall Paul
August 31st, 2016 @ 1:47 am
I found this confusing: But what if the sum of the string value and the fret is 12 or greater? In this case, you will have to subtract 12 from your sum until you get a result from 0 to 11. For example, if you press the 10 th fret of the G string, your sum is 10+10=20. Simply subtract 12 from 20 to get 8, and you see your note is F. If your result is 0, that means don’t push a fret and play the string open to get your note. Refer to the following note map and try this for other notes along the fret board: If F on the G string is fret 10 10 how do we get 8 which is an Eb. I love this whole approach but this one I am not getting for some reason Thank you
Robert
February 29th, 2016 @ 4:52 am
Good article. I have a couple of tips for helping to use this technique. The first is to check out memory pegs and method of loci to help remember the note to number lookups. I use a rhyming mnemonic for the number and an alphabetical mnemonic for the note letter then make a memorable image fusing them together e.g. Hen = 10 + Goat = G, my image being a Hen sitting on a nest of eggs on the back of a Goat. This provides an easy two-way lookup mechanism. Also you can handle the flats and sharps by finding words that end in ‘b’ and ‘sh’ and incorporating them into the mnemonic e.g. a Dab fish stuffed with Cash, allows me to combine D flat and C#. I use a Door to represent 4 in my model so I cement the association by creating a mental image of hanging a Cash-stuffed Dab off the Door handle. Weird but seems to be working. My next step is to see if I can now use the same representations to help memorise chords.
Another possible hack can help with the 12-based arithmetic by leveraging famililiarity your brain may already have dealing with a 24 hour clock. For example my brain already has a handy encoding that knows that 13 is 1 o’clock, 14 is 2 etc. If I’m looking for B I know the index number for this note is 2, so it can also be be represented by 14 (I.e. the equivalent of 2am and 2pm). Therefore I can scan the strings to find out what I need to add in terms of fret positions to get either 2 or a 14. If the open string value is 2 or lower then I can find the 2, if it’s 3 or higher then I know I need to find the 14 when travelling up the fretboard. E.g open A string is 0 so I just add two frets to get to 2; and the open G string is 10 so I need to add 4 frets to get to 14, whereas the open B string has a number of 2 already, so I don’t need to add anything, I can just play it open.
Hopefully these techniques may be of use.
Olay
September 12th, 2014 @ 10:34 pm
I had been looking for a “theoretical way” to learn the guitar chords then i stumbled on this site while helping my daughter looking for “suspension bridges”…
Nice one.
Geo. Applqst
January 24th, 2013 @ 2:48 pm
This is tremendous. I’m always looking for systems and insight rather than rote memorization like a child first learns music. Is there a reason for starting with A=0 as opposed to other possible numbers? Do you have any references to closely related info on the net or in the music literature? (If not, this is the only article of its kind.) Any ideas for tying this together with the staff, so that reading music is more streamlined, with less concern for note numbers?
ripoMann
August 27th, 2012 @ 2:45 pm
this is absolutly a mind blowing technique-awsome
Eric Polin
August 18th, 2012 @ 11:29 am
simply awesome.