Gin and Diatonic
Some of the best topic ideas come from questions asked on the Guitar Noise forums.
Unfortunately this isn’t one of them, but it was a good question,
“…I know an octave is twice the pitch of one note, for instance A is 440hz and the octave is 880hz, right? Then I was told it is “8 notes above the first” what does 8 notes above the first mean?”
Generally discussions regarding the technical frequency value of a note verses the scale name is kept under lock and key for fear of sending musicians off to the loony bin.
Let’s start with the second half of the question.
Get yourself a strong cup of coffee, we are going to discuss the fretboard.
But first, just to add to the confusion, I’m going to talk about the piano.
The piano has 88 keys. If you divide 88 by the number of notes in an octave you get…?
7 1/3 octaves
How many people came up with 11?
Well that’s because an “Oct”-ave doesn’t have 8 notes, it has 12.
This confusion is easily dealt with if you just think of the Latin root of “Octave”: “Oct” from the Latin for “Eight”. “Ave” which in Latin means “add a random number here”
I suppose you really want to know how we get 12 notes to the octave?
Take a look again at the piano. From C to C there are 12 keys each a half step apart.
“Hold on there” you say “Are you insane? There isn’t a half step from E to F and B to C, is there?”
Ahh, grasshopper the answers to your questions are “Yes I am, but I am not dysfunctional.” And “Oh yes there is.”
All of the above mentioned keys suffer from the musical version of bi-polar disorder. E# is F, Fb is E and the same goes for B and C.
Don’t ask me why. There is an advanced mathematical formula that explains why, but involves hallucinogens, moon phases and animal sacrifice. I research this every Friday at my house.
Let’s look at the fretboard.
The guitar has 6 strings and if you divide that by twelve you get .72 octaves. Which is completely wrong, but helps to explain my limited playing ability.
But seriously for just a moment, the guitar does have 6 strings, (don’t start with me, we are sticking to six), and on average the neck has 22 frets. But no you may not multiply 6 times 22 and divide by 12.
Consider tuning your guitar:
5th fret of E is the same as A
5th fret of A is the same as D
5th fret of D is the same as G
4th fret of G is the same as B
5th fret of B is the same as E
If you think about this, any note above the fret that you are tuning the next higher string to, is repeated on that higher string. In other words, the sixth fret of the E string is A#, the same note as the first fret of the A string.
Now let’s figure out the octaves.
We are going to count only the half steps/frets on each string that are not duplicated on the next higher string. (Anyone who has read David’s beginning theory articles knows that each fret is a half step. If you haven’t read them, stop reading this nonsense and go do it now.)
Here we go:
5 on E
5 on A
5 on D
4 on G
5 on B
and how many frets on the neck? That’s right – 22.
22 on E – (there is no higher string so they all count)
46 so far
I’m going to add two to the total for bending the 22nd fret of the high E string, which is a D, up to E. (Ever wonder why some guitars have that funky extra bit of fretboard extending over the soundhole? Mystery solved.)
For a grand total of, drum roll please: 48 half steps
Now you have my permission to divide that total by 12 half steps in an octave.
Did we all get four octaves?
But to answer “What does 8 notes above the first mean?” is uhh… well, from a guitar point of view the octave note is 12 half steps above the root note.
If you want to get technical, the 12 half steps are also 8 “diatonic” notes, where diatonic is a low calorie mixer. We will come back to diatonic in the section about that party animal Pythagoras.
Just for fun consider this. Here are the locations of all of the E notes on the fretboard.
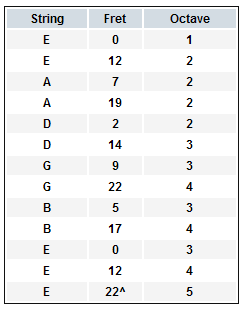
So if you are ever soloing and you want to start with E, just pull out this sheet and pick an E, any E.
“But Nick” you say, “You didn’t answer the question. 8 notes or 12, what does that mean and who picked 12 notes anyway?”
Stick with me here as we skip back to the first question.
Yes, “A” just happens to be 440Hz. That is the frequency of the sound waves hitting your ear from the source. The measure of wave peak to wave peak as they pass a given point. This doesn’t mean diddly to me really unless I’m tuning the orchestra or my guitar.
Frequency didn’t mean diddly to Bach either, his Well Tempered Clavier was a clever play on words about tuning to an exact ratio of tones divided within each octave, verses tuning to a tempered pitch to reduce overtones, and the fact that he was usually so drunk he was constantly hitting his shins on the furniture.
But before we get to Bach, let’s have a little Physics and Math lesson, shall we?
Wow, even my eyes are beginning to glaze over.
What the heck does that mean, tempered pitch verses exact ratio?
(Warning, do not read the following after 3.00 PM as it will cause your head to immediately plummet to your desk.)
Let us consider the note A, which is 440Hz.
The frequency of any component of a harmonic series can be figured using:
f(N) = N * fo
where:
N is the harmonic number
fo is the frequency of the fundamental.
We are looking for the second harmonic, which is also known as the Octave.
Hold on to your seats, here we go now,
fo = 440Hz
N = 2
So the second harmonic/octave is 880Hz.
Let’s look at the above in a different context.
Sound waves… who remembers the scene in Jurassic park where the scientist looks into the puddle and sees the ripples? The Tyrannosaurus was on his way. Time to go.
The ripples were caused by the sound wave created by the dinosaur’s footstep. They traveled through the ground and created the ripples in the puddle.
So let’s consider the T-Rex our root note frequency. Wherever he is stepping he is going to cause the ripples to move through the water at the same speed.
If you used the T-Rex ripple frequency as a base, you could figure out any other kind of dinosaur’s approach by comparing the ripples.
Now if instead of the T-Rex, it had been the dreaded “Octave-asaurus”, the ripples would move exactly twice as fast. Doubling the frequency of ripples in other words.
The “Fifth-asaurus” would send out 3 ripples in the same time as 2 T-Rex ripples.
The “Fourth-asaurus” would create 4 ripples in the same time it took for 3 T-Rex ripples.
Remember Mr. “Square of the Hypoteneuse” Pythagoras? He discovered the ratio for these harmonics, amongst other things, a couple of thousand years before Spielberg was born.
Octave = 2/1
Fifth = 3/2
Fourth =4/3
Pythagoras, who was a mathematician, came up with all of the combinations of these ratios to get numeric values for the scale.
For example:
A perfect fifth (3/2) plus a perfect fourth (4/3)
= 3*4 = 12/6 or 2/1= an octave
2*3
If you look at all the combinations of these ratios, you get the aforementioned and dreaded Pythagorean diatonic scale. In the line below big “C” is the root note and little “c” is the octave.
C=1; D=9/8; E=81/64; F= 4/3; G=3/2; A=27/16; B=243/128; c=2/1.
This is an exact ratio scale.
Pythagoras thought “Wow, harmony in music, math as harmony” until some wise guy came along and told him this system had problems. For instance, twelve pure fifths is not the same as seven octaves, but it should be.
This is called the “The cycle of Fifths” problem – not to be confused with recycling fifths, or moonshining.
Here is the “The cycle of Fifths” problem in a nutshell:
7 octaves = (2/1)^ 7 = 128
12 fifths = (3/2)^ 12 = 129.74
Let’s just walk through that in a slightly different way:
You take a note, we’ll call it the “root” and play the note a fifth above it. Now take the note you just arrived at and do the same. Repeat this a total of 12 times.
Where do you end up? Interestingly, (or not as the case may be), you end up at a note amazingly similar to your root note, 7 octaves higher.
(As an aside, and this one may take a second or two to understand, but if you flatten this series of fifths into a single octave, you get a 12-step scale. Haven’t we seen that before?)
But wait, there’s more.
If you take that note from above, the one that is 12 fifths from the root, and compare it to the original root note, taken up 7 octaves higher, well they should be exactly the same frequency, right?
Wrong.
The cycle of fifths note has a frequency of 3568.02 Hz. The octave-based note has a frequency of 3520 Hz
The difference comes from the fifth being off by .02 cents compared to the octave. Multiply this by 12 and you get an error of 24 cents or roughly a quarter semi-tone or about 48.02 Hz.
To get around this dilemma, you flatten the pitch of the fifth by 2 cents. That is a Tempered Fifth.
Why is that important?
It’s all about frequency. When you tune your guitar using harmonics and the two strings are slightly out of tune, you can hear the notes “wobble”. As you tune closer, the “wobble” decreases. As you tune further apart the “wobble” increases. Non-tempered scales do this all over the place. Say you need to play four notes simultaneously; the root, the third, the fifth and the octave. Well the root and the octave would be fine, but the third would be 14 cents flat and the fifth would be 2 cents sharp. People would run from you like you were dragging your nails down the chalkboard.
This is the reason some people argue against tuning using harmonics.
So back to Bach, his shins and his furniture…
Bach was well known around Vienna, (motto: “Sei gesegnet ohne Ende, Heimaterde, wunderhold!, translation – Birthplace of little sausages, in tins!) as a confused and drunken musician. Bach mistakenly called his shin the “Clavicle” and became an angry, belligerent drunk if you corrected him. So Bach became known as “Mr. Ill Tempered Clavicle”, Hence the play on words with Well Tempered Clavier.
Apparently at the time, there was a big debate about the use of exact ratio or tempered scale. Bach, in a moment of lucidity, wrote a prelude and fugue for each of the 12 major and minor keys – using his tempered scale. He had other tempered scales he used where 7 of the 12 fifths were tempered more and 5 were tempered less. Where the third was tempered such and such here but not there. Anyway, the first one is what we are stuck with today.
To tell the truth, Bach was only concerned with frequency as it related to the number of times he would have to urinate.
True story.
Back to reality…
Oct-ave, oct-agon, oct-upuss;
We have already seen the Latin root of the word, but Olde English is slightly different.
“oct” means 8, “ave” is old English for “it sounds like the same note but relatively higher, just please, dear God, don’t make me explain it in terms of frequency”
As you can see in the old English, music theory lessons could take a long time until they coined the word “octave”
Anyway, look at a piano or a sheet of music.
The notes go EFGABCDEFGABCDE starting at the bottom of the staff in treble clef extending up above the staff in this case. This is the singing range of the Castrati.
By the way, just in case you thought musicians were mentally stable, do a look up on the singing requirements for Castrati. I keep trying to start a Castrati choir at church, but very few ever show up for the first meeting. The ones that do are usually ex-wives whose husbands ran off with their 26 year old secretaries. They don’t want to sing, they just want to “help”.
I digress. Look back at the notes:
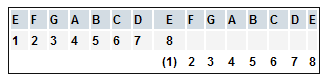
8 notes from E is E, 8 from G is G, 8 from A is A
Keep in mind you can have scales that have more or fewer notes, and often did way back when, so the number of notes to double the frequency was frequently not 8. You can argue with me here, but I will plug my ears and sing nah-nah-nah, alternating octaves without regard to frequency, just so I can’t hear you.
So the answer to the original question is:
1. Yes the octave is twice the frequency of the root note.
2. In our particular version of notation, the octave is also 8 diatonic notes above the original.
Here’s a couple of other scales to consider:
Pentatonic
Penta as in Pentagon, means five
Tonic again means a decent low calorie mixer for the copious amounts of alcohol needed to understand beginning music theory.
Advanced musical theorists no longer need tonic as they drink straight from the brown paper bag.
For the hard core musicians, (read this as Jazz), their theory helper is now measured in grams and it becomes the “pentagram” scale. When you understand this it makes it easier to understand Jazz chords.
anyway here are a major and minor movable pentatonic scale:
Based on a 5 note scale, the numbers on the frets represent the value of the note in the pentatonic scale. Some of these are octaves of each other, see above. If you notice, the fingers are moving in the same pattern, but the root has changed to protect the innocent.
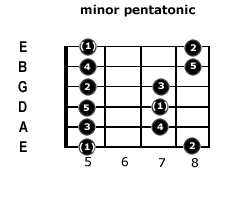
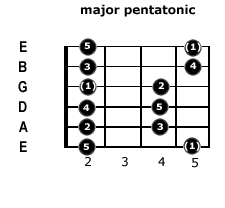
You can move these up and down the fret board changing key willy-nilly,(a Grammy winning lip syncing duo, I have no idea what they have to do with this), and the root note becomes your new key.
Classical musicians the same applies to you, just move the guitar to the other leg.
Hope this clarifies it all.
Nick
P.S. Has anyone seen my brown paper bag? Call me if you find it.
