The Power of Three
Once you have all your notes figured out and are (somewhat) familiar with scales, you’re ready to take the BIG step. Today we’re going to look at how to put together chords. But first, let’s dispense with the answers to last week’s homework:
Click here to see last weeks answers.
Like I told you last time, nothing to it, right?
Before we get going too far, you might want to take a little time to reread (or read for the first time) Jimmy Hudson’s A Study On Intervals as well as Happy New Ear. Don’t worry, we’ll wait for you to get back.
Okay? Okay.
Interval Interlude
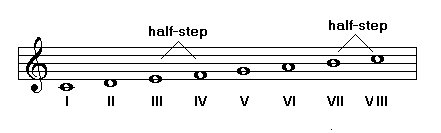
Last time out I showed you a list of all the musical notes that we have available to us. And, in case you’ve forgotten, I happen to have them right here:
You’ll recall that each one is separated by a half-step. When we arrange these notes according to a specific pattern of whole-steps and half-steps, we create a scale, like this one – our old friend, the C major scale:
Here, except in the two indicated places, the notes are separated by whole steps. The Roman numerals are indicators of the name of the interval from the root (or “I” – which in this case is C). An interval, as I’m sure you remember, is the distance between two notes. It is the basic unit of harmony. Let’s make sure we’re on the same page:
So you see that the interval from C to E is called a third. C to A is sixth. C to F is a fourth. And so on. And don’t forget that there are all the half-steps that aren’t part of the C major scale. You all know that, but let’s put them out on the table for easy reference, shall we?
Okay, are we all still here? Good, because here comes the tricky part.
The interval of the third is the key component to the assembly of chords. But, naturally, it’s not as cut and dried as we’d like to think it might be. How so? Well, let me ask you – what is the interval from C to E? Right, it’s a third. How about C to Eb? Technically, this is also a third, but we call it a minor third. A minor third is a step-and-a-half away from your starting note instead of two full steps. To distinguish between the two types of intervals, we call the “regular” third (two full steps) a major third.
This bears repeating (“…one more time!”). C to E is a major third. C to Eb is a minor third. You can see that. But let’s look at the other possible combinations available to us in the C major scale alone, shall we? Here’s the scale again (and remember the actual scale is designated with the Roman numerals):
C to E we know. C# is not part of the C major scale so we can ignore it. The next note we come to is D, so let’s look at the interval of D to F. Is it a major or minor third? Because F is three half-steps away from D it must be a minor third. Do you follow this? Start at the D and count the half steps until you reach F. E is one whole step away and the next whole step would be F#, not F. So D to F# is a major third while D to F is a minor third.
This is vital for you to know. Virtually all chord theory is based on thirds and you have to have this concept down before it will make sense to you. Let’s look at all of the possible intervals of a third that occur in the C major scale. If you want to, cover up the right hand column and test yourself:
How’d you do? Probably a lot better than you thought you might! All right, take a deep breath and get ready to tackle the final two pieces of the puzzle.
Stackables
Harmony (or disharmony (dissonance), for that matter) is created by the use of two or more notes. When two notes are played at the same time, a harmonic interval is created. If the notes are played separately so that you hear them as a sequence of notes, then we have a melodic interval. Some intervals sound pleasing to us and some are, shall we say, an acquired taste (which is the same exact phrase used by my good friends to describe my singing voice…). Major and minor thirds both fall into the “pleasant” category.
Chords are created by the use of three or more notes. And yes, this is open to debate. Some people (authorities on the subject, no less) will say that two notes are all you need to make a chord. And there actually is an argument for this, particularly if you use two notes in the interval of a fifth. But rather than getting drawn into this bit of nitpicking, let’s just say that it takes a minimum of three notes to define a specific chord. I’ve shown you this example before and it’s worth looking at again:
Here are two notes, E and G, along with their TAB locations on the guitar. Now how many chords can you name that use these two notes? Even someone who has been playing for a relatively short time should be able to name at least two and possibly upwards of four or five:
But if we add a third note, C in this case, the number of possible chords drops dramatically, as we can see:
Now, while there are other chords that use these notes, most of us see these notes and the brain automatically clicks in with “C major chord, check.”
And the C major chord will always be made up of these three notes no matter where you play them on the fretboard, as shown here:
Let’s look again at the first C major chord I showed you. In notation, it is a note on each consecutive line. This would mean that it is every other note, which we have already confirmed by stating that the chord is made up of the C, E and G notes. This method of forming a chord, basically taking one note and stacking the following two alternate notes on top of it, is the most basic form of harmony. These chords are called triads. It’s a helpful name in two respects: first, it automatically makes you think that there must be three notes in its makeup. Second, and more important, you can use the name as a way to remember how these chords are made – you take a note, add its third and then add the third of the second note.
That might be a bit confusing at first. Most people will tell you that a triad is made up of the root (“I”), the third and the fifth. And they are absolutely correct. Our example bears this out. E is the third of C and G is its fifth. But try looking at it another way, at least for a moment – E is the third of C and G is the third (albeit a minor third) of E.
There are a couple of reasons for looking at it like this. Do you remember waaaaay back when I first introduced you to primary and secondary chords of any given key? Frankly, for a while there I couldn’t remember either. But I did! It’s back in the second part of our introduction to open tuning, (Open Tuning Part 2) of all places! Do you want to know where those chords come from? They are simply triads built upon the notes of the major scale (D in that particular example). Here’s the C major scale we’ve been working with and the triads that you can make with it:
And, yes, we’ll deal with that pesky VII (what the hell is a “B diminished anyway?”) in just a bit! But first, let’s get to the real crux of today’s topic:
The Four Basic Chord Groups
Okay, now you are comfortable in distinguishing the difference between a major third and a minor third, right? Good. And you’re fine with the concept of triads, as well? Great! Let’s apply our brains for a moment then…
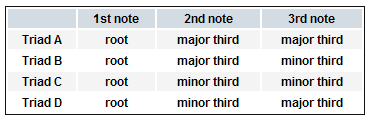
We can reason that, since triads are made by stacking a root note with its third and the subsequent third, and since there are two types of thirds at our disposal to use for this task, there must be four possible types of triads. They would look like this:
We all agree on this?
Let’s take a quick look back at the triads that we were able to make from the C major scale. All the major chords (C, F and G) are made up of a root followed by a major third and then a minor third. These chords fit the profile of “Triad B” and, if you were so inclined not to take my word for it, a quick run through all twelve major chords would prove to you that, indeed, all the major chords do. Likewise, you can see that all minor chords fit the profile of “Triad D.” Amazing how these things work out, isn’t it?
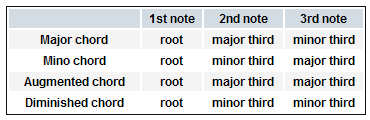
We haven’t yet covered the two remaining types of chords, but now’s as good a time as any to introduce you to them. Here’s the four basic types of chords, based on triads, and how you build them:
“Does this really work?” you might ask. Try it out for yourself and see. First get your trusty list of “all the possible notes” so you have a handy reference:
Okay! F major chord? Start with F as your root, go up a major third (A) and then go up a minor third (C). Pretty easy, huh? B minor would start with B then go up a minor third to D and then a major third to F#. This is working out rather well.
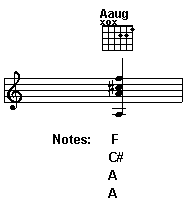
A augmented is actually a pretty chord. According to the directions, all I need to do is begin with A and then add two major thirds, which would be C# and then F. This is what it looks like on a chord chart:
Diminished chords are dark and mysterious (to me, anyway) and can add a lot of tonal color to a piece. They are difficult to put on a guitar in “root, third, fifth” format because of the way a guitar is tuned. So once you have the notes you have to come up with different shapes for them. Let’s see, a D diminished would be D (root), F (minor third) and Ab (minor third). Here would be one way to play it:
As I mentioned earlier, we will be discussing all of these chords types in the (near) future, taking special care to look at their functions in melodies, harmonies and songwriting. It should be a lot of fun.
And speaking of fun, here’s this week’s homework:
- Identify the following intervals as major or minor thirds:
- B to D#
- F to Ab
- C# to E
- E to G#
- F# to A
- Ab to C
- List the three notes that make up the following chords (you’re already given the root as part of the name!):
- C# minor
- F# major
- E augmented
- A diminished
- G augmented
- C augmented
- B major
- Bb minor
- D minor
- F diminished
- G# major
- Eb major
- C diminished
As always, please feel free to write in with any questions, comments, concerns or topics you’d like to see covered in upcoming columns. You can either drop a line at the Guitar Forums or reach me directly at [email protected]
Until next week…
Peace.









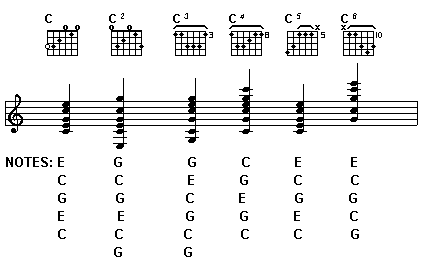



Matthew
December 19th, 2014 @ 11:24 am
Hello !
I skipped some years in the process of guitar learning, because I am always stucked with these things, and never really find useful sites where I can understand how they are working… IT’S THE BEST SITE I FOUND SO FAR, very clear and understandable lessons !
Keep up the good work, very helpful website, I want to learn guitar again :)
Pubudu
March 15th, 2012 @ 6:30 am
hii… i love your lessons… im not exactly new to music nor guitar… but my theory knowledge is definitely isn’t good enough to keep on learning.. so these are really helpful… and i would like to make a suggestion… can you put up the lessons page so that one could go through the lessons in order? sorry if there’s already such a page… i went to the lessons page and all i could find there were the new lessons you post.. thanks…
Guitar Noise Staff
March 15th, 2012 @ 8:24 am
Hey Pubudu,
If you’d like to read all the lessons that David wrote in the order he wrote them go to this page https://www.guitarnoise.com/author/davidhodge/page/93/.
Every thing is in reverse chronological order so you’ll have to go from bottom to top. Then do page 92, 91, 90 … on so on.
You’ll find things in the right order for the first 50 or 60 lessons. After that you’ll probably be a pretty decent guitar player and it won’t matter what you read next.
Thanks for the suggestion. I hope you’ll bear with us as we figure out how to organize things better.
– Paul H.