Guitar Playing By Numbers

Well, not quite.

This article started life as a stand-alone piece. However, Oleg Twerdov presented a similar piece, before mine was finished, so I offer this as another look at the same idea.

First of all, I’d just like to say that it is not a replacement for theory. It will not teach you the names of notes in scales or chords. It just offers you a way of using theory without too much thought.

Let’s start by looking at a major scale in intervals, just as Oleg did- WWHWWWH or TTSTTTS. We can translate this, directly, into frets, each one being a semi- or half-tone apart from it’s nearest neighbour. Looking at the major scale this way, gives us 2 frets, 2 frets, 1 fret, 2 frets, 2 frets, 2 frets, 1 fret.

Looking at it cumulatively, we have 0, 2, 4, 5, 7, 9, 11, 12. So, the intervals are:

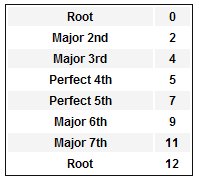
These numbers are important, so I’ll repeat them 0, 2, 4, 5, 7, 9, 11, 12.

Although what I show here is based on standard tuning, it is easily adaptable to other tunings, as it only requires that you know the number of frets between each string. In standard tuning, the guitar is tuned to perfect fourths (with apologies to the G string, which insists upon being a major third).

What, though, is the relevance of the numbers? They represent the number of frets from the root to the corresponding scale degree – and, knowing that, I can work out any scale position, without even having to know the name of the note I started from.

By applying the offset (in terms of the number of frets) to the starting position (the root), you can build a major scale anywhere on the fretboard with no trouble, at all.

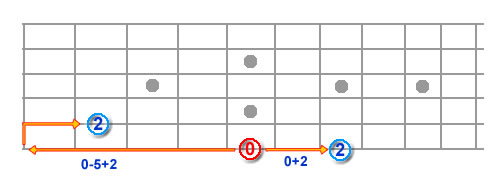
Right, let’s do just that. Let’s arrange a major scale on the fretboard, without even knowing the name of a single note. To make things easy, we’ll start with a note on the low E (6th) string – I’ll use the 5th fret (I’ve called it 6/5 – 6 th string/5 th fret). Right, we have our root note. Where do we find the 2nd degree? Two frets up from the root (just like in the table), so 6th string 7th fret (the scale so far – 6/5, 6/7).

However, because of the construction of the guitar fretboard, I can also find the same tone one string higher on the A string. Because there are 5 frets difference between the E and the A, I can take the interval away and get the number of frets LOWER on the A string – (Base + 2 frets)-5 (difference in frets between strings) = Base-3 frets, but 1 string higher. We started on the 5th fret of the low E, so the other position is 1 string higher – the A string – and 3 frets lower (5 – 3 = 2nd fret), so 5/2 (instead of 6/7, which is exactly the same pitch).

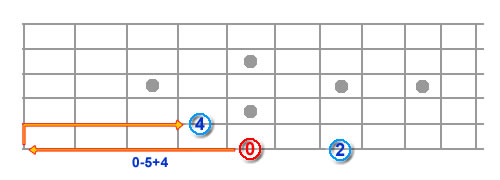
The third is 4 frets up from the root (in this case, the 5th fret) – 6/9 – but no-one is going to stretch 4 frets voluntarily. We should, therefore, look one string higher – Root+4 frets (3rd interval) -5 (frets difference between the strings) = 1 string higher and 1 fret lower (5/4). Our sequence, so far, looks like this – 6/5, 6/7, 5/4 (I could also have used 6/5, 5/2, 5/4).

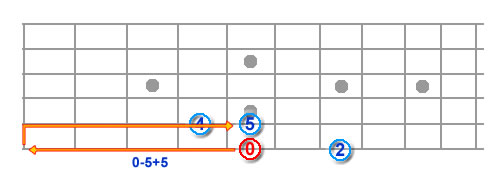
The 4th degree is 5 frets up from the root, but if no-one is going to stretch 4 frets, they’re not going attempt 5, so we have to, again, go to the next string – Root+5 frets (4th interval) -5 frets difference between the strings = same fret, but one string higher. (6/5, 6/7, 5/4, 5/5).

The 5th is 7 frets up from the root. So, Root+7-5 (frets to next string) = 2. So the 5th degree is on the next higher string and 2 frets higher than the root note. – (6/5, 6/7, 5/4, 5/5, 5/7).

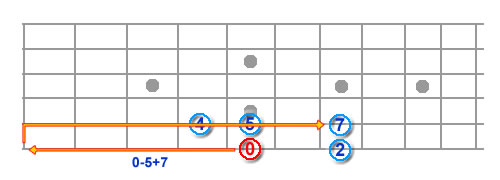
Rather than go through each calculation, let’s just jump to the octave. This is 12 frets higher than the root, so we have to factor in more than 1 string (each being 5 frets difference), i.e. Root+12-5=7, which is still too much of a stretch, so we have to take the jump to the next string and deduct another 5 frets from the answer: Root+12-5-5 = 2. So, we have to go 2 strings higher (5 + 5) and up 2 frets. – I’ve filled in the other notes in the major scale and you get this – (6/5, 6/7, 5/4, 5/5, 5/7, 4/4, 4/6, 4/7 – play it, it’s the A major scale).

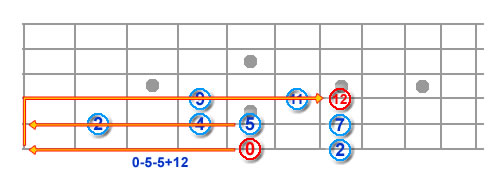
One thing that I have not yet included, in the calculation, is the G string. Don’t panic, it’s no problem. Whenever you cross the G to B string (or vice versa), you have to calculate 4 frets between strings, rather than 5. Instead of 2 strings being 5 + 5, you have to calculate 5 + 4 and find the remaining frets. So an octave is 12 – 5 – 4 = 3 – two strings and three frets higher. Why don’t you fill the major scale, that I started, all the way up to the high E string, taking care not to forget the dastardly G-B divide!

OK, here’s a table showing all the positions:

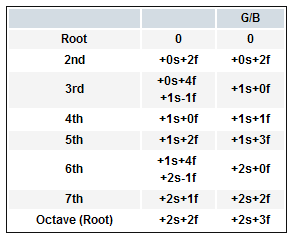
s = string, f= fret. 0= same, so 0s = same string

The column “G/B” denotes the difference, wherever the interval spans the G-B divide.

The method also allows you to work backwards – but instead of calculating from the root as 0, you call it 12. Going from the root to the 7th (found 11 frets up from the root): 12-11=1, so the 7th is 1 fret lower than the root. The calculation of moving from string to string doesn’t change. Let’s say I want to find the 4 th degree of the scale, but on a lower string than the one I’m on. For argument’s sake, we’ll assume that we’re on the root note and to make the calculation easy, at 4/7 (4 th string/7 th fret). The 4 th degree is 5 frets up from the root, so 12 (rather than 0) – 5 = 7, so 7 frets lower than my current position. I can deduct 5, to bring me one string lower: 7-5=2. I still have 2 frets left so I have to go those 2 frets lower, which takes me from the 7 th fret to the 5 th on the next lower string to where we started, so I land on 5/5.

It doesn’t stop there. Just think, you have a major chord and want to play a 7th. If you don’t know the actual fingering, you have to first work out the 7th degree of the scale that you’re in, drop it by one semitone and find that note on the fretboard.

I’ll give you another way. The 7th is 11 frets up (or 2 strings and 1 fret) from the root. A 7th chord needs a flat 7th (one semitone lower than a normal 7th or an “11b” – normal 7th is 11 frets up from the root), so we need 2 strings up and 0 frets up (0-5-5+10). I know my root note, so I can find the flat 7th 2 strings higher at the same fret. As long as it isn’t the only occurrence of a triad note (R, iii, V), I only need to fret that string at the same fret as the root note and I have a 7th chord. Alternatively, I can use the reverse calculation. A 7th is one fret lower than the root, so a flat 7th is going to be 2 frets lower. I look for a note 2 frets lower than any root, other than the bass root note. It all, of course, needs to be modified, if the G-B problem arises.

Let’s build a C7. Here is our starting point, the Cmajor chord – x32010. I need the root, two strings higher, same fret. The root is on the 5th string at the 3rd fret, so I need 3rd string, 3rd fret – yep, a classical C7. From the other standpoint – there is a root note on the B string, at the 1st fret. The method says 10 up or 2 down, but 10 up is idiocy and 2 down is somewhere the wrong side of the nut – what to do? The open B string is tuned to the same note as the 4th fret of the G string, so let’s start there. The 1st fret B string is the same as 5th fret G string, which gives us: 5-2=3, 3rd string 3rd fret.

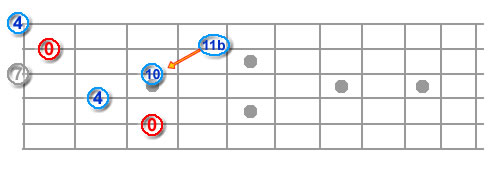
Take a Gmajor – 320003. I want a G7. So I look at the note 2 strings higher than the base root note (low E, 3rd fret), the D string – which is, unfortunately, the only occurrence of a D (5th degree) in the chord. I, then, look at another root (high E, 3rd fret) and drop 2 frets, to the 1st fret. Here is a G7 chord. This, by the way, is also 10 frets up from the root note on the 3rd string 0 fret (G): Root+10-4 (we’re crossing the G-B) -5 (B to E) =1 (1st fret, 1st string).

Once you have this in your mind, it is easy to translate any interval to the fretboard. You want a power chord? It’s made up of the root and the 5th, which is 7 frets higher than the root. Pick the root and look one string higher and 2 frets up (3, if you’re lumbered with the G-B problem). Same applies to the octave – (12 frets – 5 – 5 = 2), 2 strings higher and 2 frets ( 12 -5 – 4 = 3 for the G-B) up.

Once you have a reasonable grasp of the numbers, you can short-cut your way around the scales. How far is a 6th from a 3rd? A 6th is 9 frets up and a 3rd is 4, so the distance is 5 frets. How far is a 2nd from a flat 7th? A 7th is 11 frets up, so flatted it’s at 10. A 2nd is 2 frets up, giving us 10-2 = 8.

We can now use this knowledge to look more closely at some other scales.

The Major Scale.

What can I say? – WWHWWWH or TTSTTTS. I’ve told you how to build this.

The Minor Scales

Relative Minor – WHWWHWW

Flattens the 3rd, 6th and 7th. Easy. The sequence becomes, 0, 2, 3 (was 4, but flat, becomes 3), 5, 7, 8 (was 9, but flats to 8), 10 (was 11, but flats to 10), 12. (0,2,3,5,7,8,10,12)

Harmonic Minor – WHWWHW#H

It’s the same as the relative minor, except that the 7 th isn’t flat, which gives rise to a 3 fret gap between the 6 th and the 7 th (which I’ve shown as W#). Otherwise, it’s the relative minor – (0,2,3,5,7,8,11,12)

Melodic Minor (up) – WHWWWWH

This is the same as the major scale, but with only the 3 rd flattened, so (0,2,3,5,7,9,11,12).

Melodic Minor (down) – WHWWHW#H

Is exactly the same as the relative minor scale. (0,2,3,5,7,8,10,12)

The Major Pentatonic – WW(H+W)W(W+H)

This is the same as the major scale, with the 4th and 7th degress removed, so instead of 0, 2, 4, 5, 7, 9, 11, 12, the major pentatonic consists of 0, 2, 4, 7, 9, 12

The Minor Pentatonic

This is the same as the relative minor scale, with the 2nd and 6th degress removed, so instead of 0,2,3,5,7,8,10,12, the minor pentatonic consists of 0,3,5,7,10,12

The Modes.

Ever thought of learning the mode box patterns – after you’ve learnt the major, minor, pentatonic and God knows what other patterns, of course. No need.

Modes are just major scales, which start at different positions. Take the Mixolydian, starting at the 5th degree (7 frets up – the “base fret offset”). Just modify the calculation to deduct the base fret offset – so the root of the mixolydian is the position in the major scale minus the offset (7-7=0), the 2nd degree of the Mixo mode is really the 6th degree of the major scale, but knowing the base fret offset (7) and knowing that the 6th degree of the major scale is 9 frets up, we get 9-7=2. the second position is 2 frets higher than the “root” of our mixo scale. The 3rd is at 11 on the major scale, so 11-7=4, which is probably best one string higher, but 1 fret down (just as in the major scale layout). Next comes the 4th, which is the octave of the base major scale, but we call it 12, rather than 0, because it is the octave and not the root of the original scale: 12-7= 5, which goes on the next string, same fret. The 5th of the mixo (the 2nd of the major scale) is at 14 (octave+2), so 14-7=7 – applying the original calculation, we get 1 string and 2 frets higher.

Mixolydian mode:

You can build any mode at any starting position, without even having to memorise a single box pattern.

Whether building major scales or modes, you end up with the same patterns on the fretboard as the box patterns found in any book, but this method gives you the ability to build a scale, even if your memory is not that good and you haven’t played the pattern for several months. In fact, the more you use this method, the easier it will become to build the box patterns.

One drawback of box patterns, is that they are boxes. You learn 5, effectively, separate entities. Bringing them together and using them as one large network of notes is difficult, once you’ve learnt them separately. Another problem is that most people (and I include myself) learn the boxes as they are presented on paper, almost invariably starting with the “1st pattern” at the 6th string, 5th fret – and find that changing to play the same box somewhere else on the neck is a mental challenge. This method takes you away from building box patterns and into building scales. Try building a run from the A on the low E to the higher reaches of the high E, using box patterns. You’re going to traverse at least 2, if not 3. By selectively changing strings, you can build runs, as long as you like, on one or several strings, just by adding the necessary number of frets to your last position. This is another point – as you get better with the fret intervals, you start to think also in terms of intervals between positions, within the scale (iii – IV is 1 fret in the major scale, etc.). It is, however, the number of frets from the root, which is important – it gives you the frame of reference from which to work – the root of the scale.

Although Helgi Briem has been promoting the use of intervals for, certainly, as long as I’ve been a member of GN, this only recently hit me – it was one of those “light going on” moments. Since then I’ve found building scales much easier than with a scale chart. I’m seeing why frets are played, where they are and what relevance that position has to the rest of the scale, even if it hasn’t registered what the names of the notes are. Give it a try – it really doesn’t take long to grasp.

For those of you who say that you are lousy at maths, here’s another method – left foot is the root note, right foot is the octave and your 10 fingers (and thumbs) are the positions in between – there’s absolutely no reason NOT to give it a try now, is there? ;))