O Tannenbaum!
We’ve been doing some holiday songs the past few weeks under the guise of chord melody arrangements. In this lesson I’d like to examine another aspect of chord melodies that we’ve not spent a lot of time on and that’s looking at implied harmony. It’s nowhere near as complicated as it sounds and it’s actually something with which you’re already familiar.
Perhaps this would be a better explanation: today we’re going to do an arrangement of the traditional German Christmas carol, O Tannenbaum (known to many of us on this side of the Atlantic as O Christmas Tree), using only a melody line and a single line of harmony. That’s it, just two notes at a time. And yet these two notes will provide us with all the harmony we need.
And perhaps I should give you a little warning as well: while we will indeed be playing quite a bit in this lesson, we’re also going to be using our heads as often as, if not more often than, our fingers. Some lessons are just like that…
All right then, since we know we’re going to need the melody, let’s take a look at it, along with the chords that normally accompany the song. For the sake of making this lesson a little friendlier than it might otherwise be, we’ll do this in the key of G major. Also, since this song is learned easiest in terms of lines (lyrical lines, that is), I’ve indicated the start of each line of lyrics:
As we look as this, we should be making some assessments in regard to the piece. First off, being in the key of G, the chords are what I consider the “primary chords,” namely the I, the IV and the V. Perhaps this would be a great place to do a quick review of the key of G major. Here is its scale:
In the melody of O Tannenbaum, all of the notes belong to the G major scale. So it’s relatively safe to assume that the chord accompaniment is diatonic, meaning that all the chords are also made up solely of notes from this particular scale. Because we’ve all read The Power of Three, we can easily check that by taking each note and building a triad onto it like this:
These are all the chords that naturally occur in the key of G major. And they certainly do match up with the accompaniment that we used in Example #1. Please note that I took the liberty of making a triad for both D and D7, for reasons that will be very apparent in a short while. D7, after all, is just sticking the D note at the bottom of your F# diminished chord, or adding the C note to the D triad, whichever way you prefer to look at it. And, whether or not you know it yet, this lineup of triads is going to help us put together the arrangement for this song, so be ready to refer back to it whenever necessary!
The first note of the melody is what we call a “pick-up note.” It falls just before the first beat of the first measure. It’s also a D, which as we know is the fifth of the key of G. Going from V to I is, for most people, the aural definition of coming home (if you want to read more about this sort of thing, check out Five To One on our Guitar Column page). And the use of this interval to start the song does most of the work of establishing the tonal center of the key. What truly will nail it down, though, is the use of the third. Why is this note so important? Well, for starters, it determines whether or not we’re in G major or G minor, and that’s a fairly big difference in tone!
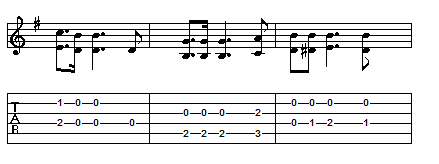
So what I want to do is to couple the G note at the start of the first full measure with a B note, which is its major third. Because I want the melody to stand out, I’ll use the B note below the melody note. That is, I’ll play the B found at the second fret of the A string instead of the one you get by playing the open B string. Try it out yourself and see which one you prefer:
As I mentioned, for the sake of this lesson I want the melody to ring out as much as possible, so I’ll keep the melody note higher in tone than the harmony note. This use of what I call “inverted” thirds (where the root is higher than the third) is done a lot on the guitar because the tuning of the instrument lends itself to this sort of voicing very well. We’ve used it in numerous lessons, such as Bookends.
Keep in mind that, since we’re using just two notes of any given chord and not the complete chord of itself, the harmony is, for all intents and purposes, implied and not spelled out for you. It’s going to be up to us to make the implications hold true to our ears.
Using the interval of the third in this way, that is, accompanying each melody note with a single third for harmony, does a great job of making our implied harmonies valid. What we’re doing here, by the way, this mirroring each note of the melody line with its respective third in the harmony line is called parallel thirds. Strictly speaking, you would want to consistently use either regular thirds or inverted thirds and not switch from one to the other. But, as you’ll soon see, that doesn’t mean you can’t!
I like the way the parallel inverted thirds sound so much that I’m going to write out the whole first phrase in this manner. To find each third, I first look at the note in question, find the note in the G scale that is two positions above it and then locate that note in on the neck lower than the melody note, thus inverting it. So, for example (and not counting the “pick up note” D), I see that A (the A on the second fret of the G string) is the second note of the melody. The third of A is C and the closest C to my A which is lower in tone than the melody is on the third fret of the A string. Let’s see what we come up with and have a listen as well:
In Version One, I strictly stick with my parallel inverted thirds and it sounds pretty good. But, and believe it or not, this comes from having written out the notation as opposed to simply playing it or writing out the TAB, I’ve found something interesting in the last two measures of this phrase. If, when the melody note is the F#, I switch the A (inverted third harmony note of Version One) to D (which I’ll have to play on the fifth fret of the A string), I create a smooth and pleasant sounding “up-and-down” bass line instead of one that simply mirrors the melody line. Take a look and see:
I hope you take the time to follow this because you might find it fascinating. And it will certainly help you if you want to be able to do your own arrangements, instead of simply playing other people’s versions of songs.
Look at the harmony line in “Version Two” and see how it climbs from C to D to E and then gently glides back down to D and then to C and B. This is called voice leading, that is, finding a harmony line that flows more naturally, step by step, instead of jumping all over the place. As far as the harmony itself goes, we haven’t changed the chord in question, nor have we deviated from our use of thirds to define the harmony. We’ve simply altered which notes of the D chord (or D7) that are serving as our harmony line. And in doing so, we’re also creating a more interesting dynamic between our melody line and our harmony line.
We’ll come back to this concept in a moment. First, though, I’d like to walk our way through the third line of the song. Structurally speaking, O Tannenbaum is very simple. This first line repeats itself as the second and final line of any given verse, so all we need do to learn the complete song is to get the middle section down. I’m going to take the liberty of dividing this section in an unusual way in order to make it easier to play:
In this section we also need to change our strategy of inverted thirds. Since the D note which starts us off is definitely part of the G chord, using the F# makes no sense at all. So we need to come up with a different note, preferably one from the G triad. We could just use the G (the open G string itself), but I think we’ll get better results from looking at our melody note and then adding whatever note of the G scale that happens to be a third below it. In other words, D is the third of B, so let’s use B as our harmony note. This will certainly work for the first part of this phrase (the third line of lyrics for this song).
When we get to the second half of this phrase (the fourth line of lyrics) though, ironically enough at the next appearance of the D in the melody line, we’ll need to revert back to our original use of inverted thirds in order to stay on the D7 chord.
The fingering of this can be difficult, so I’d like to recommend you also examine other ways to play it. I like to play the first half of this section, line three, on just the B and G strings and then switch to playing the notes that begin line four on the G and D strings, like this:
I find that this fingering of line four makes going from the “regular thirds” to the inverted thirds particularly smooth, especially since it means just keeping a finger on the F# note! You may find ways that work better for you. And you should definitely try anything that comes to mind.
Now that we’ve gotten this section of the Christmas carol worked out, we can play the entire thing. Shall we give it a try?
Sounds pretty decent, no? But you know better than to think that we’re done with our lesson for today, don’t you? Of course, you do!
One of the fascinating things about working in implied harmony is how easy it is to change the “implied” part of the harmony. Do me a favor and play these notes:
Okay, what chord is this? You’re bound to say “D7,” simply because we’ve been using these notes in this context in this particular song. But, hearing these two notes just by themselves and not in the context of a song, what keeps us from saying “A minor” or even “F major?”
This is why context and voice leading can be incredibly important to an arrangement. Let’s throw out our “chord sheet” for a moment and look at two ways of playing Line Three:
That last pair of notes, the C in the melody and the A in the harmony line, definitely sound like A minor now, don’t they? We can find the reason for this back at the very beginning of O Tannenbaum. Remember the D that serves as the pick-up note and how that V to I drove home the G major tonality? There’s a reason that five to one is called a “perfect cadence.” And we’re doing the same thing here but in a more devious fashion. We’re temporarily giving the song a new tonality – that of A minor. This, in the terms of music theory, is called modulation. By using a G# with the D note of the melody, we create an E7 chord, which is the V in the key of A minor. Pretty cool, no? If you want to read more about this sort of thing, we’ve numerous articles on Guitar Noise that deal with it. Five To One (or “Home Home Again”) is a good place to start.
This modulation worked so well here, let’s do another one. How about during the last line of the song?
Here we’re making the song modulate to E minor by using, guess what! Yes, by raising the D note in our harmony line up a half step to D#, we are implying a B major chord and we all know that B is the V chord in the key of E minor. It’s amazing what tonal color you can add by changing a single note of harmony, even if your single note of harmony is the melody’s sole accompaniment! And it adds a bit of depth when you go back to the “normal” playing of the song. Your ears are now not hearing simple major chord changes because they are ready to accept implied minor chords, seventh chords and a host of other possibilities.
Just for the record (and kudos to those of you with eagle eyes!) I often “exaggerate” or stress this particular modulation when I play it. How? By simply altering the rhythm of the phrase into straight eighth notes! It’s a simple yet effectively dynamic device.
Most of the time, people don’t even bother to analyze things like these modulations and implied harmonies, and sometimes it’s probably just as well. Single line voice leading is a lot of fun but you can get so bogged down in the theory that you miss out on interesting chances. Here’s Line Four to give us an example:
In this phrase, I’ve used an F natural note to create an interesting chromatic bass line. It certainly fits in well and sounds terrific. But what implied harmony have I created? In the notation I’ve chosen to call it “Dm” but I could have easily called it “F” as well. This is probably best thought of as a “passing tone,” namely a note whose purpose is simply to get us from point A to point D, no pun intended. Well, maybe…
The objective in this example was not to create a modulation, but rather to have an ear catching harmony line that was both interesting and functional. You can get into all sorts of debates, theory-wise, as to the function of this note, but the important thing here is to listen to what you’ve created. Does it work? Does it seamlessly add to the harmony of your arrangement or bring things to a crashing halt? Well, let’s listen to all the chromatic variations we’ve come up with as part of the song:
I think you’ll agree with me that we’ve done a great job of making the song more interesting without causing anyone to sit up and wonder what happened to good ol’ O Tannenbaum!
And I hope that you enjoyed this lesson, even if it was a little bit more on the cerebral side. Remember that the more you experiment and, far more important, the more music that you listen to, the more interesting the arrangements you might be able to come up with.
And until our next lesson, let me leave you with what is probably a lousy translation of the third verse of this carol:
O Christmas tree, o Christmas tree
Your faithful leaves will teach me
That hope and faith and constancy
Give peace and strength eternally
O Christmas tree, o Christmas tree
Your faithful leaves will teach me
Peace.






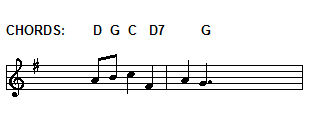


























tom nelson
April 27th, 2014 @ 5:38 pm
Very good explanation of chord melody playing